资产市场简介

资产市场是基于AI科学计算平台构建的开发者生态社区，致力于提供科研、生物医药、化学材料、流体仿真等多个领域的华为自研及开源的多元化工具套件，包括小分子药物设计和Notebooks。旨在提供一个安全、开放的环境，促进资产的共享与使用，从而加速生物医药、基因组分析、化学材料等领域的应用开发和实际应用。保障开发生态链上各参与方高效地实现各自的商业价值。

平台提供的资产如表1和表2所示。

表1 小分子药物设计资产列表
领域	资产类别	资产名称	描述
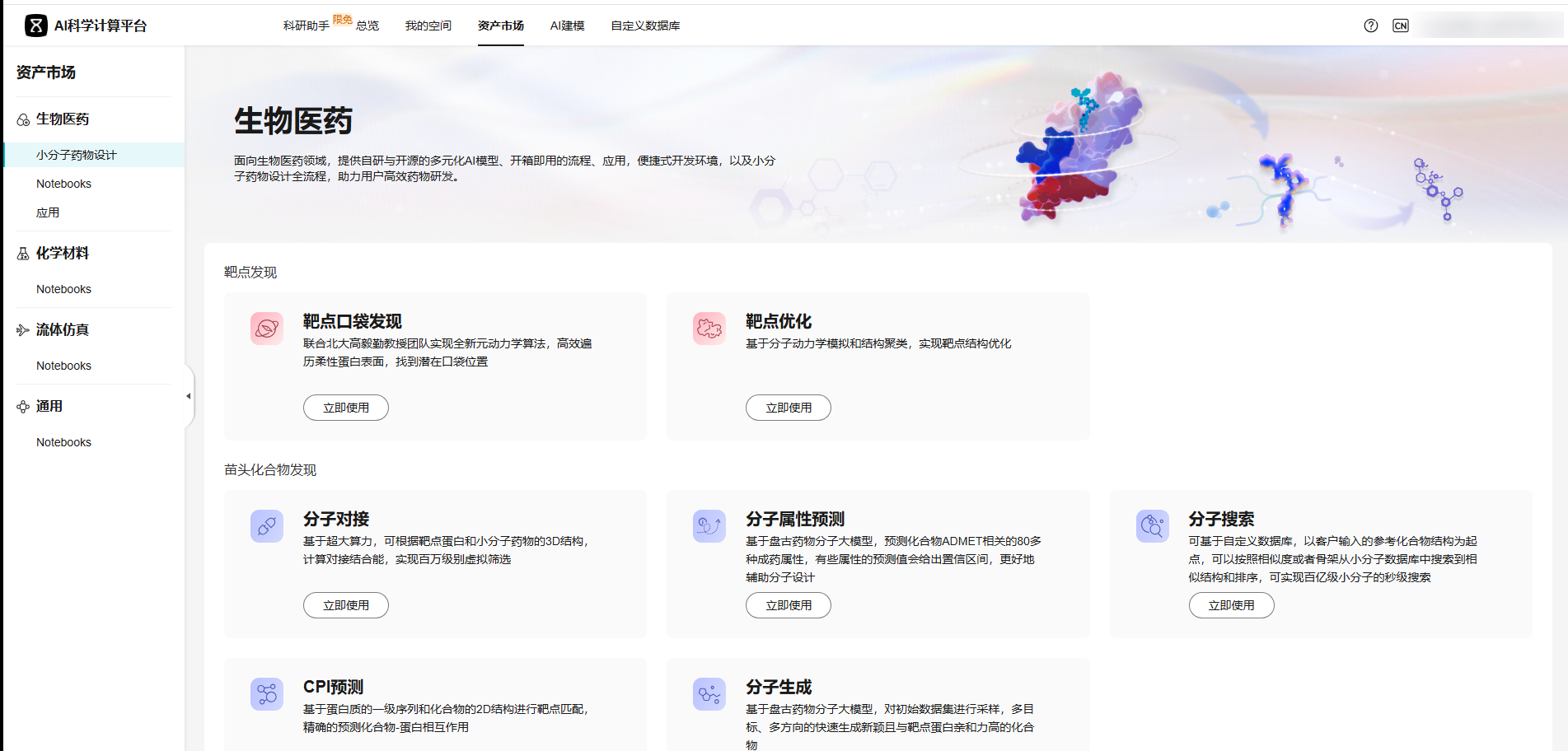
生物医药	靶点发现	靶点口袋发现	联合北大高毅勤教授团队实现全新元动力学算法，高效遍历柔性蛋白表面，找到潜在口袋位置。
	靶点发现	靶点优化	基于分子动力学模拟和结构聚类，实现靶点结构优化。
	苗头化合物发现	分子对接	基于超大算力，可根据靶点蛋白和小分子药物的3D结构，计算对接结合能，实现百万级别虚拟筛选。
		分子属性预测	基于盘古药物分子大模型，预测化合物ADMET相关的80多种成药属性，有些属性的预测值会给出置信区间，更好地辅助分子设计。
		分子搜索	可基于自定义数据库，以客户输入的参考化合物结构为起点，可以按照相似度或者骨架从小分子数据库中搜索到相似结构和排序，可实现百亿级小分子的秒级搜索。
		CPI预测	基于蛋白质的一级序列和化合物的2D结构进行靶点匹配，精确的预测化合物-蛋白相互作用。
		分子生成	基于盘古药物分子大模型，对初始数据集进行采样，多目标、多方向的快速生成新颖且与靶点蛋白亲和力高的化合物。
	先导化合物优化	分子优化	基于盘古药物分子大模型，以参考化合物为起点，针对给定的期望理化性质，得到性质更优、结构新颖、与靶点蛋白亲和力高的化合物。
		靶点口袋分子设计	基于盘古药物分子大模型，从靶点口袋出发，从头生成与口袋具有高亲和力、结构新颖的化合物。
		自由能微扰	基于纯国产分子动力学模拟库SPONGE，产生自动化FEP工作流，端到端计算配体修饰造成的亲和能改变。
	通用工具	MOL 3D Viewer	Mol 3D Viewer工具查看蛋白质和小分子的3D结构。
		MOL Editor	Mol Editor工具可以查看小分子的2D结构。
		聚类分析	通过骨架聚类方法，将小分子数据库中结构相似的化合物聚成一类，从而可以找到有效骨架，辅助苗头化合物发现。

表2 镜像资产列表
领域	资产名称	说明
生物医药	GenomeAgent	端到端自动化生物信息流程AI智能体，基于大模型的生物信息知识及代码生成能力，以提示词工程为框架自动编写任务计划和代码。
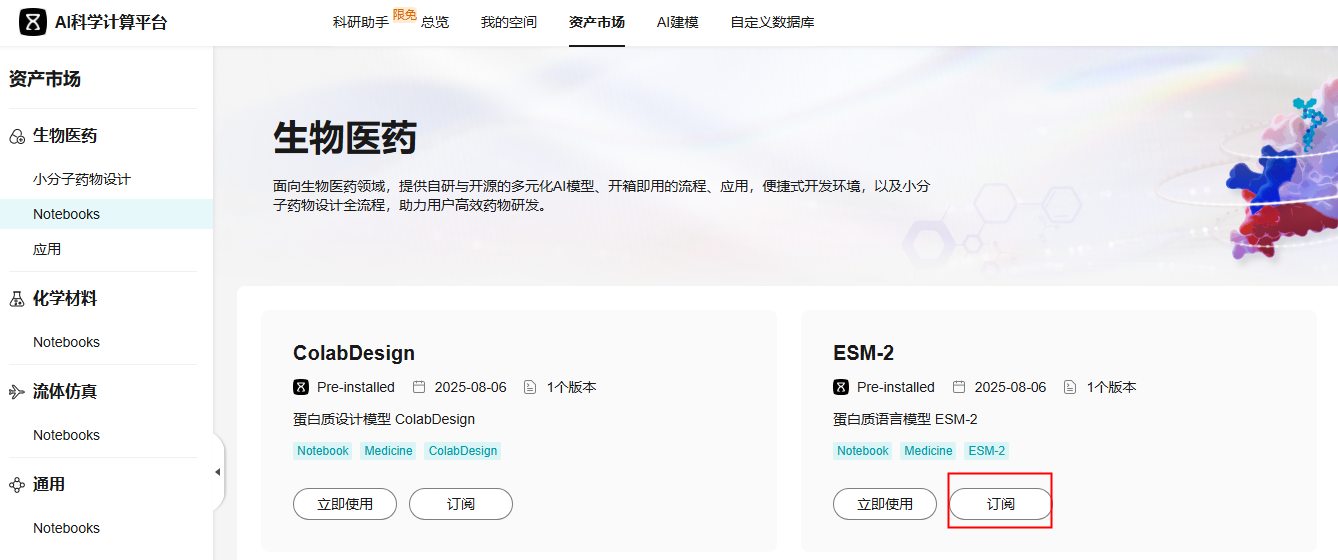
	ESM-2	ESM-2是基于transformer的蛋白质语言模型，使用注意力机制来学习输入序列中氨基酸对之间的相互作用。
	ProteinMPNN	ProteinMPNN是一种基于深度学习的蛋白质序列设计方法，给定一个蛋白质的backbone结构，预测能折叠成该结构的氨基酸序列。该模型广泛应用于蛋白质设计领域。
	ColabDesign	ColabDesign是蛋白质设计模型，通过输入蛋白质骨架坐标的pdb文件，基于蛋白质结构预测模型来预测整个蛋白质序列。
	UFold	UFold是一种基于深度学习的RNA二级结构预测方法，基于一种全新的类图像RNA序列表示方法，通过全卷积网络(Fully Convolutional Networks, FCNs)高效地进行RNA二级结构预测。
化学/材料	DeephE3nn	DeephE3nn是一个基于E3的等变神经网络，利用晶体中的原子结构去预测体系的电子哈密顿量。
	DiffCSP	DiffCSP是基于图神经网络和等变扩散模型的晶体生成模型，基于给定组分，实现预测晶体材料的结构。
	Allegro	Allegro是基于等变图神经网络构建的模型，可以在材料体系中进行高精度分子能量预测。
	NequIP	NequIP是基于等变图神经网络构建的模型，根据分子体系中各原子的位置与原子数信息构建图结构描述，进行分子势能与力的预测。
	Matformer	Matformer是基于图神经网络和Transformer架构的模型，用于预测晶体材料的性质。
流体仿真	FNO2D-NS	纳维-斯托克斯方程（Navier-Stokes equation）是计算流体力学领域的经典方程，是一组描述流体动量守恒的偏微分方程，简称N-S方程。该资产利用Fourier Neural Operator（FNO）学习某一个时刻对应涡度到下一时刻涡度的映射，实现二维不可压缩N-S方程的求解。
	FNO3D-NS	纳维-斯托克斯方程（Navier-Stokes equation）是计算流体力学领域的经典方程，是一组描述流体动量守恒的偏微分方程，简称N-S方程。该资产利用三维傅里叶神经算子对纳维-斯托克斯方程（Navier-Stokes equation）进行求解。
	PINNs-Burgers1D	基于物理驱动的PINNs (Physics Informed Neural Networks)方法，求解一维有粘性情况下的Burgers方程。
	PINNs-CylinderFlow	利用 PINNs 方法学习位置和时间到相应流场物理量的映射，实现纳维-斯托克斯（Navier-Stokes, NS）方程的求解，从而解决圆柱绕流的尾流流场问题。
	PINNs-Periodic-Hill	雷诺平均Navier-Stokes方程求解周期山流动问题是流体力学和气象学领域中的一个经典数值模拟案例，该资产采用雷诺平均模型模拟湍流在二维周期山地地形上的流动。
	PINNs-Kovasznay	基于物理信息神经网络（PINNs）方法来求解Kovasznay流动问题。
	PINNs-Taylor-Green	在流体力学中，Taylor-Green涡流动是一种不稳定的衰减的涡流，在二维周期性边界条件时存在精确解，该精确解与Navier-Stokes方程的解一致。该资产使用PINNs对二维的taylor green涡流进行仿真。
	KNO2D-NS	纳维-斯托克斯方程（Navier-Stokes equation）是计算流体力学领域的经典方程，是一组描述流体动量守恒的偏微分方程，简称N-S方程。该资产利用Koopman Neural Operator学习某一个时刻对应涡度到下一时刻涡度的映射，实现二维不可压缩N-S方程的求解。
	KNO1D-Burgers	伯格斯方程（Burgers’ equation）是一个模拟冲击波的传播和反射的非线性偏微分方程，被广泛应用于流体力学，非线性声学，气体动力学等领域。一维伯格斯方程（1-d Burgers’ equation）的应用包括一维粘性流体流动建模。
	FNO1D-Burgers	计算流体力学是21世纪流体力学领域的重要技术之一，其通过使用数值方法在计算机中对流体力学的控制方程进行求解，从而实现流动的分析、预测和控制。传统的有限元法（finite element method，FEM）和有限差分法（finite difference method，FDM）常用于复杂的仿真流程（物理建模、网格划分、数值离散、迭代求解等）和较高的计算成本，往往效率低下。因此，借助AI提升流体仿真效率是十分必要的。
	PINNs-Darcy	达西方程（Darcy equation）是一个描述了流体在多孔介质中低速流动时渗流规律的二阶椭圆型偏微分方程，被广泛应用于水利工程，石油工程等领域中。达西方程最初由亨利·达西根据沙土渗流实验的实验结果制定，后来由斯蒂芬·惠特克通过均质化方法从纳维-斯托克斯方程推导出来。本案例利用PINNs求解二维定常达西方程。
	SNO1D-Burgers	伯格斯方程（Burgers’ equation）是一个模拟冲击波的传播和反射的非线性偏微分方程，被广泛应用于流体力学，非线性声学，气体动力学等领域。一维伯格斯方程（1-d Burgers’ equation）的应用包括一维粘性流的建模。
	SNO2D-NS	利用Spectral Neural Operator（SNO）学习某一个时刻对应涡度到下一时刻涡度的映射，实现二维不可压缩N-S方程的求解。
	SNO3D-NS	纳维-斯托克斯方程（Navier-Stokes equation）是计算流体力学领域的经典方程，是一组描述流体动量守恒的偏微分方程，简称N-S方程。该资产利用三维SNO神经算子对纳维-斯托克斯方程（Navier-Stokes equation）进行求解。
	AI-Turbulence	湍流AI模型是基于昇腾AI开发的面向航空航天工程高雷诺数问题的高精度AI仿真模型，并在昇思MindSpore流体仿真套件的支持下，建立了大型客机机翼、翼身组合体等千万网格量级全尺度应用级大规模并行智能化的高效湍流模拟方法。
	PDE-Net	PDE-Net是一种前馈深度网络用于从数据中学习偏微分方程，同时实现了准确预测复杂系统的动力学特性和揭示潜在的PDE模型。PDE-Net的基本思想是通过学习卷积核(滤波器)来逼近微分算子，并应用神经网络或其他机器学习方法来拟合未知的非线性响应。
	PeRCNN	物理嵌入递归卷积神经网络（Physics-encoded Recurrent Convolutional Neural Network，PeRCNN），基于结合部分物理先验设计的π-卷积模块，通过特征图之间的元素乘积实现非线性逼近。该物理嵌入机制保证模型严格服从给定的物理方程。所提出的方法可以应用于有关PDE系统的各种问题，包括数据驱动建模和PDE的发现，并可以保证准确性和泛用性。
通用	Torch-NPU	包含以下环境信息：python-3.9、torch-2.3.1、torch-npu 2.3.1
	MindSpore	包含以下环境信息：python-3.9、MindSpore-2.3.1
	MindFormer	包含以下环境信息：python-3.9、MindSpore-2.3.1、MindFormers-1.2.0
	R-Notebook	包含以下环境信息：R 4.1.0

表3 应用列表
领域	资产名称	说明
生物医药	GenomeAgent	端到端自动化生物信息流程AI智能体应用，基于大模型的生物信息知识及代码生成能力，以提示词工程为框架自动编写任务计划和代码。整体功能与Notebook版的镜像功能一致，区别点在于APP应用暴露了基本的入参和出参，支持从黑盒层面进行使用，同时支持API创建作业。