流体仿真
面向流体仿真领域,提供AI加持的多种计算模拟工具,支持求解多种流体控制方程,高效使能航空航天、船舶制造、能源电力等行业的工程设计。
资产列表
|
领域 |
资产类型 |
资产名称 |
说明 |
|---|---|---|---|
|
流体仿真 |
镜像 |
FNO2D-NS |
纳维-斯托克斯方程(Navier-Stokes equation)是计算流体力学领域的经典方程,是一组描述流体动量守恒的偏微分方程,简称N-S方程。该资产利用Fourier Neural Operator(FNO)学习某一个时刻对应涡度到下一时刻涡度的映射,实现二维不可压缩N-S方程的求解。 |
|
FNO3D-NS |
纳维-斯托克斯方程(Navier-Stokes equation)是计算流体力学领域的经典方程,是一组描述流体动量守恒的偏微分方程,简称N-S方程。该资产利用三维傅里叶神经算子对纳维-斯托克斯方程(Navier-Stokes equation)进行求解。 |
||
|
PINNs-Burgers1D |
基于物理驱动的PINNs (Physics Informed Neural Networks)方法,求解一维有粘性情况下的Burgers方程。 |
||
|
PINNs-CylinderFlow |
利用 PINNs 方法学习位置和时间到相应流场物理量的映射,实现纳维-斯托克斯(Navier-Stokes, NS)方程的求解,从而解决圆柱绕流的尾流流场问题。 |
||
|
PINNs-Periodic-Hill |
雷诺平均Navier-Stokes方程求解周期山流动问题是流体力学和气象学领域中的一个经典数值模拟案例,该资产采用雷诺平均模型模拟湍流在二维周期山地地形上的流动。 |
||
|
PINNs-Kovasznay |
基于物理信息神经网络(PINNs)方法来求解Kovasznay流动问题。 |
||
|
PINNs-Taylor-Green |
在流体力学中,Taylor-Green涡流动是一种不稳定的衰减的涡流,在二维周期性边界条件时存在精确解,该精确解与Navier-Stokes方程的解一致。该资产使用PINNs对二维的taylor green涡流进行仿真。 |
||
|
KNO2D-NS |
纳维-斯托克斯方程(Navier-Stokes equation)是计算流体力学领域的经典方程,是一组描述流体动量守恒的偏微分方程,简称N-S方程。该资产利用Koopman Neural Operator学习某一个时刻对应涡度到下一时刻涡度的映射,实现二维不可压缩N-S方程的求解。 |
||
|
KNO1D-Burgers |
伯格斯方程(Burgers’ equation)是一个模拟冲击波的传播和反射的非线性偏微分方程,被广泛应用于流体力学,非线性声学,气体动力学等领域。一维伯格斯方程(1-d Burgers’ equation)的应用包括一维粘性流体流动建模。 |
||
|
FNO1D-Burgers |
计算流体力学是21世纪流体力学领域的重要技术之一,其通过使用数值方法在计算机中对流体力学的控制方程进行求解,从而实现流动的分析、预测和控制。传统的有限元法(finite element method,FEM)和有限差分法(finite difference method,FDM)常用于复杂的仿真流程(物理建模、网格划分、数值离散、迭代求解等)和较高的计算成本,往往效率低下。因此,借助AI提升流体仿真效率是十分必要的。 |
||
|
PINNs-Darcy |
达西方程(Darcy equation)是一个描述了流体在多孔介质中低速流动时渗流规律的二阶椭圆型偏微分方程,被广泛应用于水利工程,石油工程等领域中。达西方程最初由亨利·达西根据沙土渗流实验的实验结果制定,后来由斯蒂芬·惠特克通过均质化方法从纳维-斯托克斯方程推导出来。本案例利用PINNs求解二维定常达西方程。 |
||
|
SNO1D-Burgers |
伯格斯方程(Burgers’ equation)是一个模拟冲击波的传播和反射的非线性偏微分方程,被广泛应用于流体力学,非线性声学,气体动力学等领域。一维伯格斯方程(1-d Burgers’ equation)的应用包括一维粘性流的建模。 |
||
|
SNO2D-NS |
利用Spectral Neural Operator(SNO)学习某一个时刻对应涡度到下一时刻涡度的映射,实现二维不可压缩N-S方程的求解。 |
||
|
SNO3D-NS |
纳维-斯托克斯方程(Navier-Stokes equation)是计算流体力学领域的经典方程,是一组描述流体动量守恒的偏微分方程,简称N-S方程。该资产利用三维SNO神经算子对纳维-斯托克斯方程(Navier-Stokes equation)进行求解。 |
||
|
AI-Turbulence |
湍流AI模型是基于昇腾AI开发的面向航空航天工程高雷诺数问题的高精度AI仿真模型,并在昇思MindSpore流体仿真套件的支持下,建立了大型客机机翼、翼身组合体等千万网格量级全尺度应用级大规模并行智能化的高效湍流模拟方法。 |
||
|
PDE-Net |
PDE-Net是一种前馈深度网络用于从数据中学习偏微分方程,同时实现了准确预测复杂系统的动力学特性和揭示潜在的PDE模型。PDE-Net的基本思想是通过学习卷积核(滤波器)来逼近微分算子,并应用神经网络或其他机器学习方法来拟合未知的非线性响应。 |
||
|
PeRCNN |
物理嵌入递归卷积神经网络(Physics-encoded Recurrent Convolutional Neural Network,PeRCNN),基于结合部分物理先验设计的π-卷积模块,通过特征图之间的元素乘积实现非线性逼近。该物理嵌入机制保证模型严格服从给定的物理方程。所提出的方法可以应用于有关PDE系统的各种问题,包括数据驱动建模和PDE的发现,并可以保证准确性和泛用性。 |
使用说明
下面以 FNO2D-NS 资产为例,阐述如何使用资产镜像创建Notebook进行使用。
- 进入“资产市场”,单击资产卡片下方“订阅”按钮,即可订阅该资产到空间进行使用。
单击资产卡片,可跳转至资产详情页,可查看资产详细描述以及使用说明。
图1 资产订阅 图2 资产详情页
图2 资产详情页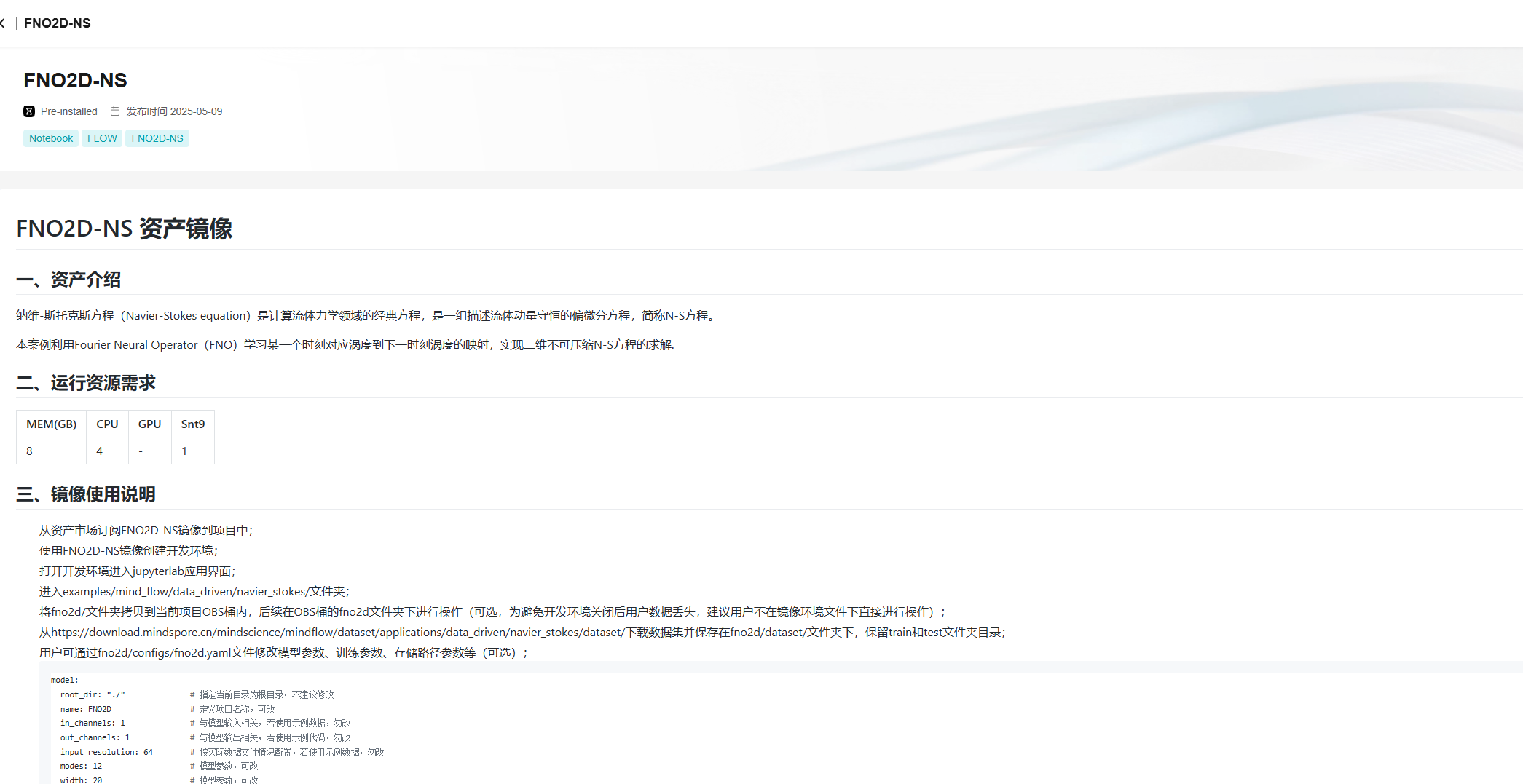
- 进入空间,在“我的空间 > 镜像”页面的列表中,可以查看已订阅的镜像资产。
图3 已订阅镜像
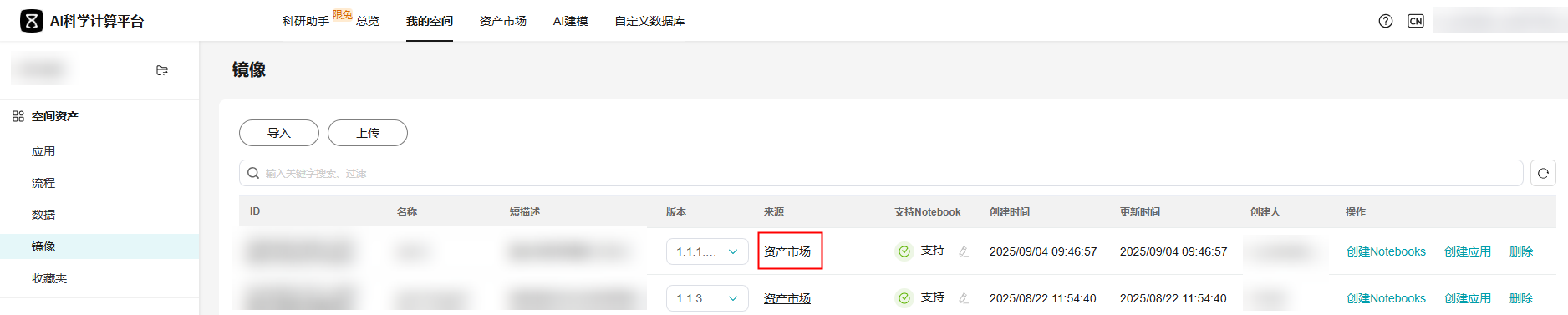
- 进入“我的空间 > Notebooks”页面,单击“创建Notebooks”,镜像类型选择“自定义”,选择资产市场已订阅的FNO2D-NS镜像,并设置合适的计算资源数量以及存储挂载路径。
图4 创建Notebook
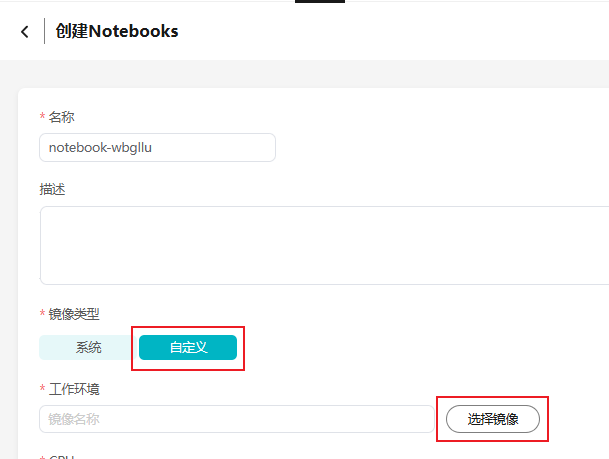 图5 选择自定义镜像
图5 选择自定义镜像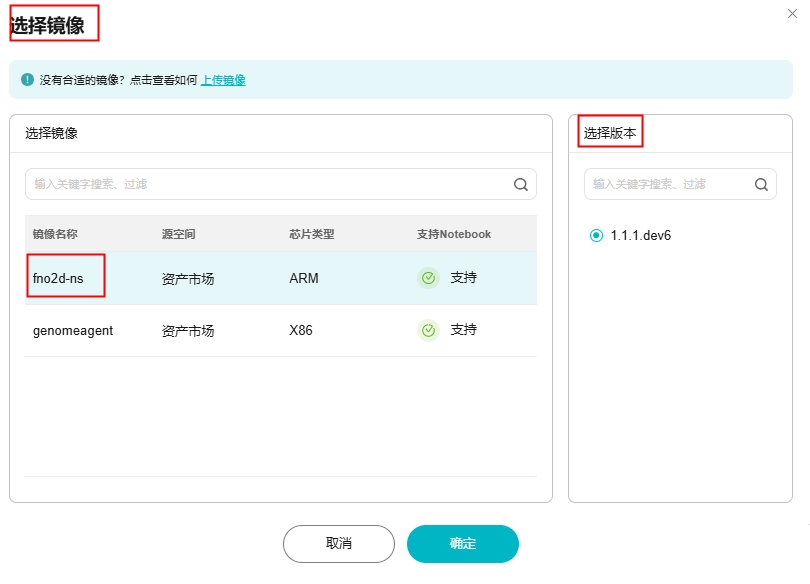 图6 设置计算资源
图6 设置计算资源
- 打开创建成功的Notebook,参考资产详情页的使用说明进行使用即可。






