数学优化求解器
运筹优化算法基于实际约束场景(如成本和收益、可用资源和需求、目标和限制等),运用数学规划和元启发式算法等多种优化引擎找到最佳的解决方案,去解决实际问题。
运筹优化算法的主要研究对象是各种有组织的管理问题及其生产经营活动,算法的目的是针对所研究的对象求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到实际需求的最优目标。
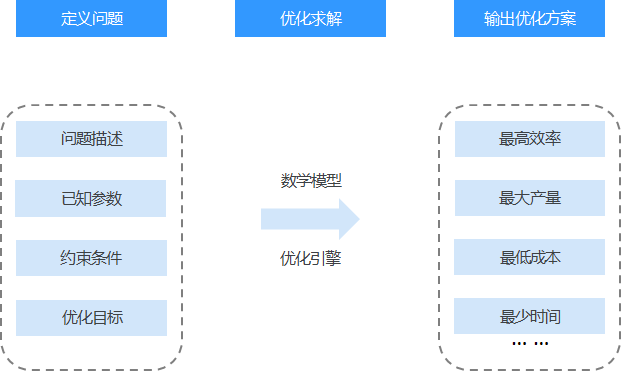
运筹优化算法总结为定义问题、优化求解、输出优化方案,如图1所示。
定义问题
根据业务的需求,一般需要定义的问题内容包括问题描述、已知参数、约束条件、优化目标。
问题描述:运筹优化算法所要解决的实际问题描述,例如计划生产的产品收益等。
已知参数:解决问题过程中的已知参数,例如生产原料,具备不同技能的生产工人、各种生产机器等。
约束条件:解决问题过程中的约束条件,例如每台机器不能连续生产20小时,每个工人不能连续工作16小时等。
优化目标:待解决的问题目标,例如最大化生产利润、最低运营成本等。
优化求解
把问题的输入,即需求、资源、约束条件、求解目标用一定的数学模型表示出来,然后通过数学规划和元启发式算法等多种优化引擎对模型求解。
输出优化方案
通过对数学模型的优化求解,将获得一个最优方案,用于解决实际问题。
支持功能
|
数学规划求解器 |
求解性能 |
LP/MIP求解性能,3万约束3.5万变量50万非零元规模的问题,平均求解时间在10分钟内 |
|
支持问题类型 |
支持求解大规模线性问题、二次型问题和混合整数线性问题。 需具备对多种算法模型的兼容性,以满足行业多样化业务场景的要求,支持线性、非线性、混合整数、二次约束规划等算法模型的建模和求解 |
|
|
支持算法 |
支持优先级和权重的控制,具备单纯形法、内点法、分支定界算法等能力 |
|
|
并行运算 |
支持并行运算,允许同时进行多个算法的求解,支持多优化任务接口同时调用的业务场景 |
|
|
接口友好 |
提供方便易用的多种主流语言接口,包括Java、Python、C++SDK接口以及命令行、lp/mps文件等多种API接口调用 |